Class 12 Electric Charges and Fields Important Questions 2025

Class 12 Electric Charges and Fields Important Questions

Struggling with Class 12 Electric Charges and Fields Important Questions before your exam? Want to know what kind of problems are most likely to appear in your physics paper this year? Let’s explore the most crucial questions that can make a big difference in your CBSE board results.

This post covers all key questions from Class 12 Physics Chapter 1 Electric Charges and Fields, including derivations, conceptual problems, and numerical questions. These are picked based on past year trends, CBSE guidelines, and expert insights. From Coulomb's Law to electric dipole fields, we’ve got you covered.

Dr. H.C. Verma and NCERT solutions both point toward the importance of mastering these concepts. So, let’s dive straight into the top-scoring questions that every Class 12 physics student should practice right now!

Question 1.
Why must the electrostatic field be normal to the surface at every point of a charged conductor?

Answer:
That tangent on a charged conductor gives the direction of the electric field at that point.

Question 2.
Why should the electrostatic field be zero inside a conductor?

Answer:
The electrostatic field inside a conductor should be zero because of the absence of charge. As in a static condition, the charge remains only on the surface.

Question 3.
A charge ‘q’ is placed at the centre of a cube of side l. What is the electric flux passing through each face of the cube? 

Answer:
Electric flux through each phase of the cube

Question 4.

Define electric dipole moment. Write its SI unit.

Answer:
The electric dipole moment of an electric dipole is defined as the product of the magnitude of either charge and the dipole length.

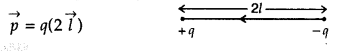
S.I. unit of dipole (p⃗ ) is coulomb metre (Cm).

Question 5.
Which orientation of an electric dipole in a uniform electric field would correspond to stable equilibrium?

Answer:
When the dipole moment vector is parallel to the electric field vector
P→∥E→

Question 6.
If the radius of the Gaussian surface enclosing a charge is halved, how does the electric flux through the Gaussian surface change?

Answer:
Electic flux ϕE is given by
ϕE=∮E→⋅ds⃗ =Qε0
…. where [Q is the total charge inside the closed surface
∴ On changing the radius of the sphere, the electric flux through the Gaussian surface remains the same.

Question 7.
Define the term electric dipole moment of a dipole. State its SI unit.

Answer:
τ = OE sin θ
If E = 1 unit, θ = 90°, then τ = P
Dipole moment may be defined as the torque acting on an electric dipole, placed perpendicular to a uniform electric dipole, placed perpendicular to a uniform electric field of unit strength.
The strength of an electric dipole is called the dipole moment.
|P→|=q|2a|
∴ SI unit is Cm.

Question 8.
In which orientation, a dipole placed in a uniform electric field in

• stable,
• unstable equilibrium?

Answer:

• For stable equilibrium, a dipole is placed parallel to the electric field.
• For unstable equilibrium, a dipole is placed antiparallel to the electric field.

Question 9.
The figure shows three point charges, +2q, -q, and + 3q. Two charges +2q and -q are enclosed within a surface ‘S’. What is the electric flux due to this configuration through the surface ‘S’.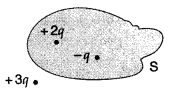

Answer: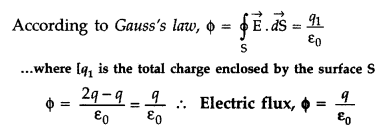
 Electric flux =∮SE→⋅dS−→

Question 10.
Name the physical quantity whose SI unit is JC-1. Is it a scalar or a vector quantity?

Answer:

• Physical quantity whose SI unit is JC-1 is Electric potential.
• It is a Scalar quantity.

Question 11.
A charge ‘q’ is placed at the centre of a cube of side l. What is the electric flux passing through two opposite faces of the cube? 
Answer:
ϕE=q3ε0

Question 12.
Depict the direction of the magnetic field lines due to a circular current-carrying loop.
Answer:
The direction of the magnetic field lines is given by the right-hand thumb rule.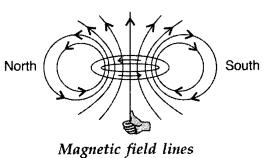

Question 13.
What is the direction of the electric field at the surface of a charged conductor having charge density σ < 0? 
Answer:
The direction of the electric field is normal and inward to the surface.

Question 14.
Why do the electric field lines not form closed loops? 
Answer:
Electric field lines do not form closed loops because the direction of an electric field is from positive to negative charge. So, one can regard a line of force starting from a positive charge and ending on a negative charge. This indicates that electric field lines do not form closed loops.

Question 15.
Is the electric field due to a charge configuration with total charge zero, necessarily zero? Justify. 
Answer:
No, it is not necessarily zero. If the electric field due to a charge configuration with total charge is zero, because the electric field due to an electric dipole is non-zero.

Question 16.
Two charges of magnitudes 2Q and + +Q are located at points (a, 0) and (4a,0) respectively. What is the electric flux due to these charges through a sphere of radius ‘3a’ with its centre at the origin? 

Answer:

Question 17.
Two charges of magnitudes 3Q and + 2Q are located at points (a, 0) and (4a, 0), respectively. What is the electric flux due to these charges through a sphere of radius ‘5a’ with its centre at the origin?
Answer: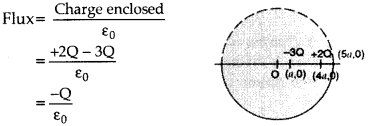

Question 18.
Write the expression for the work done on an electric dipole of dipole moment p in turning it from its position of stable equilibrium to a position of unstable equilibrium in a uniform electric field E. 
Answer:
Torque, acting on the dipole, is τ = pE sin θ

Question 19.
Why do the electrostatic field lines not form closed loops? 
Answer:
Electric field lines do not form closed loops because the direction of an electric field is from positive to negative charge. So, one can regard a line of force starting from a positive charge and ending on a negative charge. This indicates the electric field. Lines do not form closed loops.

Question 20.
Why do the electric field lines never cross each other? 

Answer:
The electric lines of force give the direction of the electric field. In case two lines of force intersect, there will be two directions of the electric field at the point of intersection, which is not possible.

Question 21.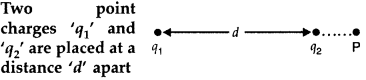

distance d apart as shown in the figure. The electric field intensity is zero at a point ’P’ on the line joining them as shown. Write two conclusions that you can draw from this. 
Answer:

• Two point charges ‘ q1‘ and ‘ q2 should be of opposite nature.
• The magnitude of charge q1 must be greater than that of charge q2.

Question 22. What is the electric flux through a cube of side 1 cm that encloses an electric dipole? 
Answer:
Zero because the net charge of an electric dipole (+ q and – q) is zero.

Question 23.
Why are electric field lines perpendicular at a point on an equipotential surface of a conductor? 
Answer:
If the electric field lines were not normal to the equipotential surface, they would have a non-zero component along the surface. To move a unit test charge against the direction of the component of the field, work would have to be done, which means this surface cannot be an equipotential.
Hence, electric field lines are perpendicular at a point on an equipotential surface of a conductor.

Question 24.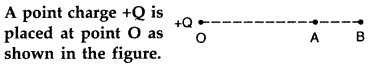

Is the potential difference VA – VB positive, negative, or zero? 
Answer:
The potential difference is positive.

Question 25.
How does the electric flux due to a point charge enclosed by a spherical Gaussian surface get affected when its radius is increased?
Answer:
The electric flux due to a point charge enclosed by a spherical Gaussian surface remains ‘unaffected’ when its radius is increased.

Question 26.
Show on a plot the nature of variation of the

• Electric field (E) and
• potential (V) of a (small) electric dipole with the distance (r) of the field point from the centre of the dipole. 

Answer: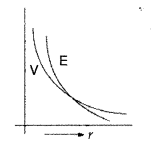

Question 27.
Does the charge given to a metallic sphere depend on whether it is hollow or solid? Give a reason for your answer. 
Answer:
No, it does not, because the charge resides only on the surface of the conductor.

Question 28.
Draw a plot showing the variation of the electric field with distance from the centre of a solid conducting sphere of radius R, having a charge of +Q on its surface.
Answer:
Plot between E and r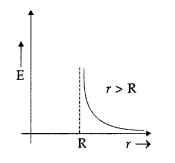

Question 29.
A point charge +Q is placed in the vicinity of a conducting surface. Draw the electric field lines between the surface and the charge.
Answer: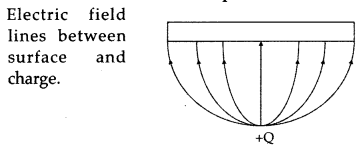

Question 30.
Derive an expression for the torque experienced by an electric dipole kept in a uniform electric field. 
Answer:
Consider an electric dipole consisting of charges + +q and -q and of length 2a placed in a uniform electric field 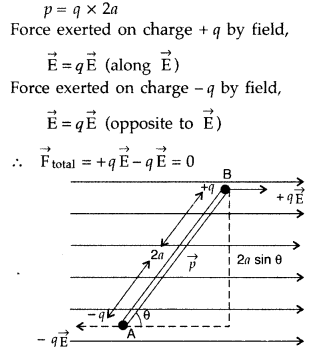E→ making an angle θ with it. It has a dipole moment of magnitude,

Hence, the net translating force on a dipole in a uniform electric field is zero. But the two equal and opposite forces act at different points of the dipole. They form a couple that exerts a torque.
Torque = Either force × Perpendicular distance between the two forces
x = qE × 2a sin θ

X = pE sin θ [ ∵ p = q × 2a; p is dipole moment]
As the direction of torque τ
⃗  is perpendicular to p⃗  and E⃗ , so we can write τ⃗ =p⃗ ×E→

Question 31.
Define electric flux. Write its SI unit.
A charge q is enclosed by a spherical surface of radius R. If the radius is reduced to half, how would the electric flux through the surface change? 
Answer:
Electric flux over an area in an electric field is the total number of lines of force passing through the area. It is represented by ϕ. It is a scalar quantity. Its SI unit is Nm2 C-1 or Vm.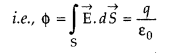

Electric flux ϕ by q enclosed
Hence, the electric flux through the surface of the sphere remains the same.

Question 32.
A spherical conducting shell of inner radius r1 and outer radius r2 has a charge ‘Q’. A charge ‘q’ is placed at the centre of the shell.
(a) What is the surface charge density on the
(i) inner surface,
(ii) outer surface of the shell?
(b) Write the expression for the electric field at a point x > r2 from the centre of the shell.

Answer:
(a) Surface charge density on the :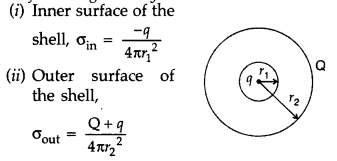

(b) Electric field at a point x > r2 from the centre of the shell will be E = 14πε0(q+Qx2)

Question 33.
Show that the electric field at the surface of a charged conductor is given by E→=σε0n^, where σ is the surface charge density and h is a unit vector normal to the surface in the outward direction. 
Answer:
Electric field at a point on the surface of a charged conductor, E = 14πε0QR2
For simplicity, we consider a charged conductor as a sphere of radius ‘R’. If ‘σ’ is in surface charge density, then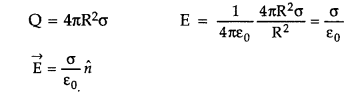

…where [ n^ is a unit vector normal to the surface in the outward direction]

Question 34.
A thin, straight, infinitely long conducting wire having charge density X is enclosed by a cylindrical surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder. 
Answer:
Since the field is everywhere radial, flux through the two ends of the cylindrical Gaussian surface is zero. At the cylindrical part of the surface, E is normal to the surface at every point, and its magnitude is constant, since it depends only on r. The surface area of the curved part is 2πrl, where l is the length of the cylinder.

Flux through the Gaussian surface = Flux through the curved cylindrical part of the surface is zero. At the cylindrical part of the surface, E is normal to the surface at every point, and its magnitude is constant, since at every point, and its magnitude is constant, since it depends only on r. The surface area of the cylinder.

Flux through the Gaussian surface = Flux through the curved cylindrical part of the surface
= E × 2πrl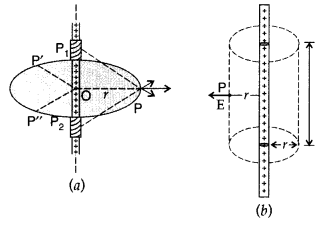

(a) The electric field due to an infinitely long, thin straight wire is radial.
(b) The Gaussian surface for a long, thin wire of uniform linear charge density
The surface includes a charge equal to λl.
Gauss’s law then gives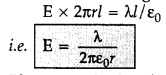

Question 35.
Plot a graph showing the variation of coulomb force (F) versus (1r2), where r is the distance between the two charges of each pair of charges : (1µC, 2µC) and (2µC, – 3µC). Interpret the graphs obtained. 
Answer: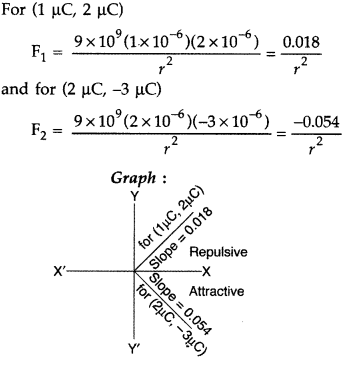

Here positive slope depicts that the force is repulsive in nature, and a negative slope depicts that the force is attractive in nature.

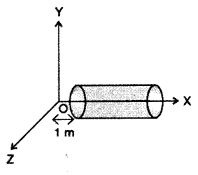
Question 36.
A hollow cylindrical box of length 1m and area of cross-section 25 cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by E→=50xi^ where E is in NC-1 and x is in metres. Find

• Net flux through the cylinder.
• Charge enclosed by the cylinder.

Answer: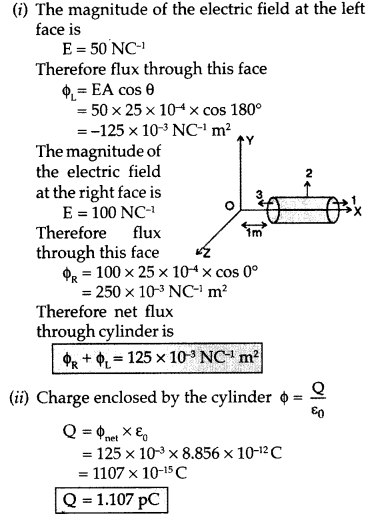

Question 37.
Given a uniform electric field , find the flux of this field through a square of 10 cm on a side whose plane is parallel to the y-z plane. What would be the flux through the same square if the plane makes a 30° angle with the x-axis? 

Answer:
Given: E→=5×103i^N/C
A = 10 × 10 × 10-4m2,
Flux (ϕ) = EA cos θ
(i) For first case, θ = 0, cos 0 = 1
∴ Flux = (5 × 103) × (10 × 10 × 10-4)
(ii) Angle of square plane with x-axis = 30°
Hence the 0 will be 90° – 30° = 60°
EA cos θ = (5 × 103) × (10 × 10 × 10-4) × cos 60
= 50 × 12
= 25 Nm2C-1

Question 38.
Given a uniform electric field E→ = 2 × 103 i^ N/ C, find the flux of this field through a square of side 20 cm, whose plane is parallel to the y-z plane. What would be the flux through the same square if the plane makes an angle of 30° with the x-axis? 
Answer:
Given: E→=5×103i^N/C
A = 10 × 10 × 10-4m2,
Flux (ϕ) = EA cos θ
(i) For first case, θ = 0, cos 0 = 1
∴ Flux = (5 × 103) × (10 × 10 × 10-4)
(ii) Angle of square plane with x-axis = 30°
Hence the 0 will be 90° – 30° = 60°
EA cos θ = (5 × 103) × (10 × 10 × 10-4) × cos 60
= 50 × 12
= 25 Nm2C-1
Hint : (i) 80 Nm2C-1
(ii) 40 Nm2C3

Question 39.
Given a uniform electric field E→=4×103i^ N/C. Find the flux of this field through a square of 5 cm on a side whose plane is parallel to the Y-Z plane. What would be the flux through the same square if the plane makes a 30° angle with the x-axis? 

Answer:
Given: E→=5×103i^N/C
A = 10 × 10 × 10-4m2,
Flux (ϕ) = EA cos θ
(i) For first case, θ = 0, cos 0 = 1
∴ Flux = (5 × 103) × (10 × 10 × 10-4)
(ii) Angle of square plane with x-axis = 30°
Hence the 0 will be 90° – 30° = 60°
EA cos θ = (5 × 103) × (10 × 10 × 10-4) × cos 60
= 50 × 12
= 25 Nm2C-1
Hint:
(i) 10 Nm2C-1
(ii) 5 Nm2C-1

Question 40.
A small metal sphere carrying charge +Q is located at the centre of a spherical cavity in a large uncharged metallic spherical shell. Write the charges on the inner and outer surfaces of the shell. Write the expression for the electric field at the point P1.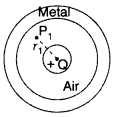

Answer:

1. Charge on inner surface: – Q
2. Charge on outer surface: + Q
3. Electric field at point P1 (E) = 14πε0Qr21

Question 41.
An electric dipole is placed in a uniform electric field E→ with its dipole moment p⃗  parallel to the field. Find
(i) the work done in turning the dipole till its dipole moment points in the direction
opposite to E→.
(ii) the orientation of the dipole for which the torque acting on it becomes maximum.
Answer: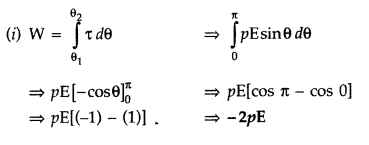

(ii) τ = p⃗ ×E→ = pE sin θ
For θ = π2, sin θ = 1 and τ is maxximum

Question 42.
A sphere S1 of radius r1 encloses a net charge Q. If there is another concentric sphere S2 of radius r2 (r2 > r) enclosing charge 2Q, find the ratio of the electric flux through S1 and S2. How will the electric flux through sphere S1 change if a medium of dielectric constant K is introduced in the space inside S2 in place of air?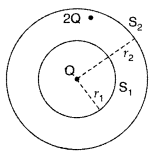 

Answer: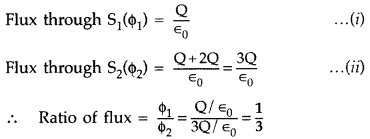

Therefore, there will be no change in the flux through S1 on introducing a dielectric medium inside the sphere S2.

Question 43.
Define the term ‘electric flux’. Write its SI units. What is the flux due to the electric field E→=3×103i^ N/C through a square of side 10 cm, when it is held normal to it?
Answer:

Electric flux over an area in an electric field is the total number of lines of force passing through the area. It is represented by ϕ. It is a scalar quantity. Its S.I unit is Nm2 C-1 or Vm.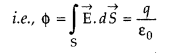

Electric flux ϕ by q enclosed
Hence, the electric flux through the surface of the sphere remains the same.

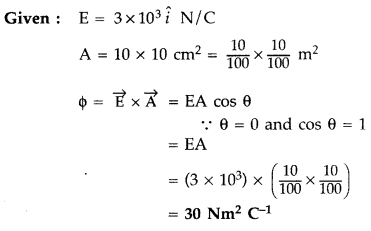
Question 44.
A thin conducting spherical shell of radius R has charge Q spread uniformly over its surface. Using Gauss’s law, derive an expression for the electric field at a point outside the shell.
Draw a graph of electric field E(r) with distance r from the centre of the shell for 0 ≤ r ≤ ∞
Answer:
Electric field at a point outside the shell :
(a) (i) To find out the electric field at a point outside a spherical charged shell, we imagine a symmetrical Gaussian surface in such a way that the point lies on it.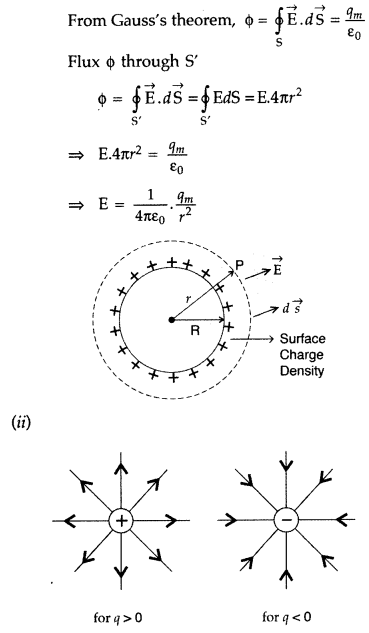

Graph of electric field E(r) :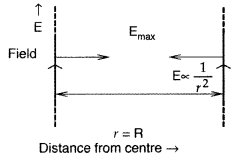

Question 45.
State Gauss’ law in electrostatics. Using this law, derive an expression for the electric field due to a uniformly charged infinite plane sheet.
Answer:
Gauss’ Law states that “the total flux through a closed surface is 1ε0 times the net charge enclosed by

Let σ be the surface charge density (charge per unit area) of the given sheet, and let P be a point at distance r from the sheet where we have to find 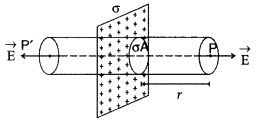E→

Choosing point P’, symmetrical with P on the other side of the sheet, let us draw a Gaussian cylindrical surface cutting through the sheet as shown in the diagram. As at the cylindrical part of the Gaussian surface, 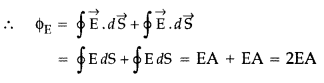E→ and dS→ are at a right angle, the only surfaces having E→ and dS→ parallel are the plane ends

…[As E is outgoing from both plane ends, the flux is positive.
This is the total flux through the Gaussian surface.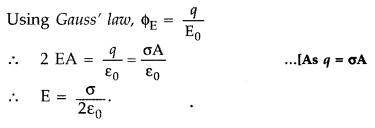

This value is independent of r. Hence, the electric field intensity is the same for all points near the charged sheet. This is called uniform electric field intensity.

Question 46.
State Gauss' law’ in electrostatics. Use this law to derive an expression for the electric field due to an infinitely long straight wire of linear charge density λ cm-1
Answer:
Gauss’s law in electrostatics: It states that “the total electric flux over the surface S in vacuum is 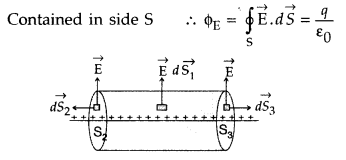1ε0 times the total charge (q).”

Electric field due to an infinitely long straight wire: Consider an infinitely long straight line charge having linear charge density X to determine its electric field at a distance r. Consider a cylindrical Gaussian surface of radius r and length l coaxial with the charge. By symmetry, the electric field E has the same magnitude at each point of the curved surface S1 and is directed radially outward.
Total flux through the cylindrical surface,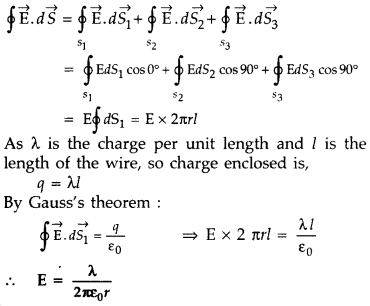

Question 47.
A positive point charge (+ q) is kept in the vicinity of an uncharged conducting plate. Sketch electric field lines originating from the point onto the surface of the plate.
Derive the expression for the electric field at the surface of a charged conductor. 

 Answer:

Representation of the electric field. (due to a positive charge)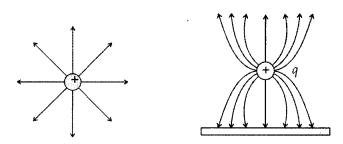

Question 48.
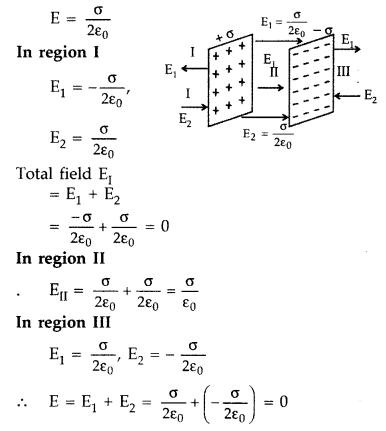
Use Gauss’s law to derive the expression for the electric field between two uniformly charged large parallel sheets with surface charge densities a and -a, respectively. 
Answer:

Gauss’ Law states that “the total flux through a closed surface is 1ε0 times the net charge enclosed by

Let σ be the surface charge density (charge per unit area) of the given sheet and let P be a point at distance r from the sheet where we have to find E→

Choosing point P’, symmetrical with P on the other side of the sheet, let us draw a Gaussian cylindrical surface cutting through the sheet as shown in the diagram. As at the cylindrical part of the Gaussian surface, 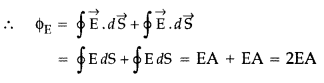E→ and dS→ are at a right angle, the only surfaces having E→ and dS→ parallel are the plane ends

…[As E is outgoing from both plane ends, the flux is positive.
This is the total flux through the Gaussian surface.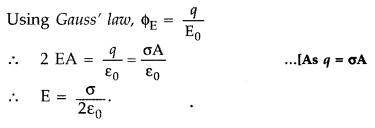

This value is independent of r. Hence, the electric field intensity is same for all points near the charged sheet. This is called uniform electric field intensity.

Question 49.
State Gauss’s law.
A thin straight infinitely long conducting wire of linear charge density ‘X’ is enclosed by a cy¬lindrical surface of radius V and length ‘l’—its axis coinciding with the length of the wire. Obtain the expression for the electric field, indi¬cating its direction, at a point on the surface of the cylinder.
Answer:
Gauss’s law. Gauss' law states that “Total flux (electric flux) over the closed surfaces in vacuum is He0 times the total charge (Q) contained inside S.”

Since the field is everywhere radial, flux through the two ends of the cylindrical Gaussian surface is zero. At the cylindrical part of the surface, E is normal to the surface at every point, and its magnitude is constant, since it depends only on r. The surface area of the curved part is 2πrl, where l is the length of the cylinder.

Flux through the Gaussian surface = Flux through the curved cylindrical part of the surface is zero. At the cylindrical part of the surface, E is normal to the surface at every point, and its magnitude is constant, since at every point, and its magnitude is constant, since it depends only on r. The surface area of the cylinder.

Flux through the Gaussian surface = Flux through the curved cylindrical part of the surface
= E × 2πrl

(a) Electric field due to an infinitely long thin straight wire is radial.
(b) The Gaussian surface for a long thin wire of uniform linear charge density
The surface includes charge equal to λl.
Gauss’s law then gives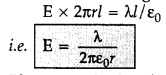

Question 50.
(a) Define electric flux. Write its S.I. units.
(b) Consider a uniform electric field
E→ = 3 × 103 i^ N/C. Calculate the flux of this field through a square surface of area 10 cm2 when
(i) its plane is parallel to the y-z plane, and
(ii) the normal to its plane makes a 60° angle with the x-axis. 
Answer:
(a)
Electric flux over an area in an electric field is the total number of lines of force passing through the area. It is represented by ϕ . It is a scalar quantity. Its S.I unit is Nm2 C-1 or Vm.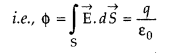

Electric flux ϕ by qenclosed
Hence the electric flux through the surface of sphere remains same.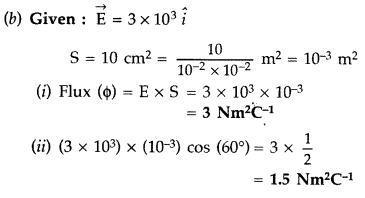

Question 51.
Two charged spherical conductors of radii R1 and R2 when connected by a conducting wire acquire charges q1 and q2 respectively. Find the ratio of their surface charge densities in terms of their radii. 
Answer:
Two charged spherical conductors of radii R1 and R2 when connected by a conducting wire acquire charges q1 and q2 respectively. Thus these two conductors have a common potential V.
Two charged spherical conductors of radii R1 and R2 when connected by a conduction wire acquire charges q1 and q2 respectively. Thus these two conductors have a common potential V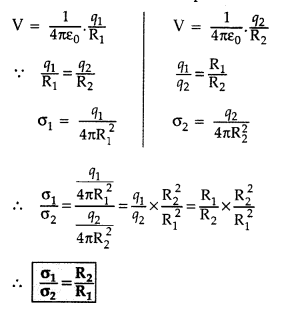

Question 52.
Two point charges + q and -2q are placed at the vertices ‘B’ and ‘C’ of an equilateral triangle ABC of side as given in the figure. Obtain the expression for (i) the magnitude and (ii) the direction of the resultant electric field at the vertex A due to these two charges.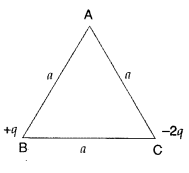


Answer: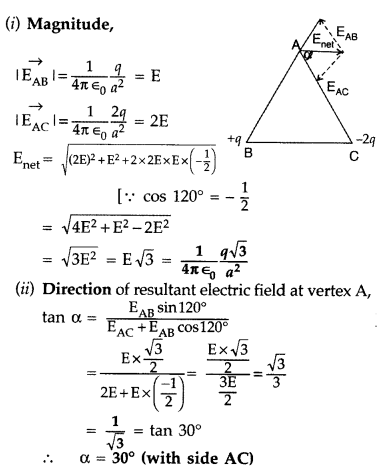

Question 53.
Two point charges + 3q and – 4q are placed at the vertices ‘B’ and ‘C’ of an equilateral triangle ABC of side ‘a’ as given in the figure. Obtain the expression for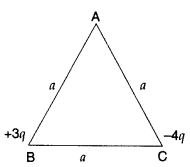

(i) the magnitude and
(ii) the direction of the resultant electric field at the vertex A due to these two charges. 
Answer: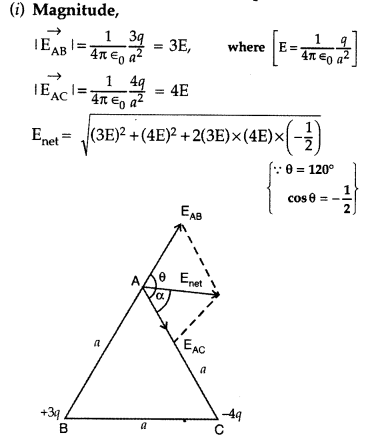

Question 54.
An electric dipole of dipole moment p→ is placed in a uniform electric field E→?. (a) Obtain the expression for the torque τ→experienced by the dipole. (b) Identify two pairs of perpendicular vectors in the expression. 
Answer:
(a) Torque on electric dipole. Consider an electric dipole consisting of two equal and opposite point charges separated by a small distance 2a having dipole moment

So the net force on the dipole is zero
Since "E" it is uniform, the dipole does not undergo any translatory motion.

These forces being equal, unlike, and parallel, from a couple, which rotates the dipole in a clockwise direction
∴ Magnitude of torque = Force × arm of the couple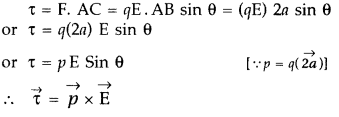

[The direction of τ⃗  is given by right hand screw rule and is normal to p⃗   ] and E⃗ 
Special cases
(i) when θ = 0 then τ = PE sin θ = 0
∴ Torque is zero and the dipole is in stable equilibrium
(ii) When θ = 90 then τ = PE sin 90 = PE
∴ The Torque is maximum
(b) Ratio of flux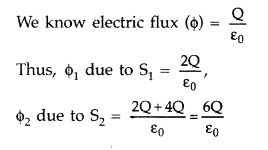


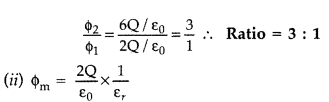
∴ Electric flux through the sphere S1 decreases with the introduction of dielectric inside it.

(b) Two pairs of perpendicular vectors are,
* τ→ is perpendicular to p→
* τ→is perpendicular to E→

Question 55.
(a) Two spherical conductors of radii Ra and R2 (R2 > R1) are charged. If they are connected by a conducting wire, find out the ratio of the surface charge densities on them.
(b) A steady current flows in a metallic conductor of non-uniform cross-section. Which of these quantities is constant along the conductor: current, current density, electric field, or drift speed? 

Answer:
(a) When two charged spherical conductors of Radii R1 and R2 respectively (R2 > R1) are connected by a conducting wire, we know that the common potential (V) is given by,

Question 56.
A charge is distributed uniformly over a ring of radius ‘a’. Obtain an expression for the electric intensity E at a point on the axis of the ring. Hence show that for points at large distances from the ring, it behaves like a point charge.

Answer:
Electric Intensity on the axis of a ring:

This is the Electric Field due to a point charge at a distance x.

Question 57.
Two thin concentric and coplanar spherical shells, of radii a and b (b > a) carry charges, q and Q, respectively. Find the magnitude of the electric field at a point distant x, from their common centre for
(i) 0 < x < a
(ii) a ≤ x < b
(iii) b ≤ x < ∞ 

 Answer: Magnitude of Electric field: Two thin concentric and coplanar spherical shells of radii ‘a and ‘b’ (b > a) carry charges ‘q’ and ‘Q’ respectively.
(i) For 0 < x < a
The point lies inside both the spherical shells.
Hence, E(x) = 0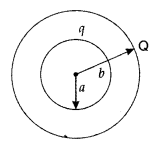

(ii) For a ≤ x < b
Point is outside the spherical shell of radius ‘a’ but inside the spherical shell of radius ‘b’.
∴ E(x) = 14πε0⋅qx2
(iii) For b ≤
x < ∞
Point is outside of both the spherical shells. Total effective charge at the centre equals (Q + q).
E(x) = 14πε0⋅(q+Q)x2

Question 58.
A charge +Q is uniformly distributed within a sphere of radius R. Find the electric field, due to this charge distribution, at a point distant r from the centre of the sphere where :
(i) 0 < r < R and
(ii) r > R 

Answer:
We have

Question 59.
(i) Derive the expression for the electric field at a point on the equatorial line of an electric dipole.
(ii) Depict the orientation of the dipole in
(a) stable,
(b) unstable equilibrium in a uniform electric field. 

Answer:

(I) Electric dipole moment: It is the product of the magnitude of either charge and the distance between them.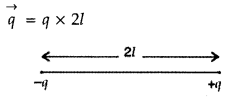

It is a vector quantity whose direction is from negative to positive charge.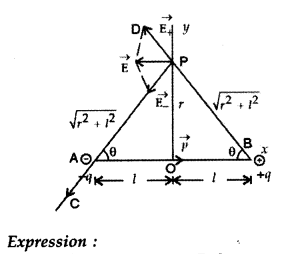

Electric field intensity at P due to +q charge is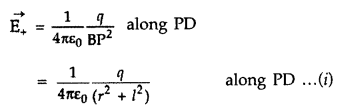

Electric field intensity at P due to -q charge is,

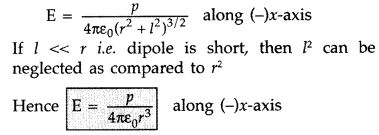
(ii) (a) For stable equilibrium, the angle between p and E is 0°,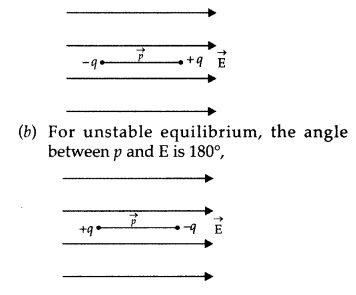

(b) For unstable equilibrium, the angle between p and E is 180°,

Question 60.
(i) Obtain the expression for the torque τ⃗  experienced by an electric dipole of dipole moment p⃗  in a uniform electric field E→?
(ii) What will happen if the field were not uniform?

Answer:
(i)
(a) Torque on electric dipole. Consider an electric dipole consisting of two equal and opposite point charges separated by a small distance 2a, having a dipole moment

So the net force on the dipole is zero
Since "E" is uniform, the dipole does not undergo any translatory motion.

These forces being equal, unlike, and parallel, from a couple, which rotates the dipole in clockwise direction
∴ Magnitude of torque = Force × arm of the couple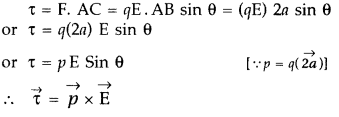

[The direction of τ⃗  is given by right hand screw rule and is normal to p⃗   ] and E⃗ 
Special cases
(i) when θ = 0 then τ = PE sin θ = 0
∴ Torque is zero, and the dipole is in stable equilibrium
(ii) When θ = 90 then τ = PE sin 90 = PE
∴ The Torque is maximum
(b) Ratio of flux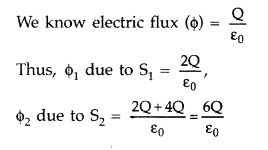


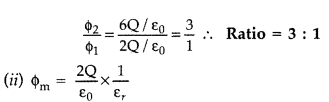
∴ Electric flux through the sphere S1 decreases with the introduction of a dielectric inside it.

(ii) If the electric field is non-uniform, the dipole experiences a translatory force as well as a torque.

Question 61.
State Gauss’s law in electrostatics. Derive an expression for the electric field due to an infinitely long straight uniformly charged wire. 

Answer:
Gauss's Theorem: The surface integral of the electric field over a closed surface is equal to 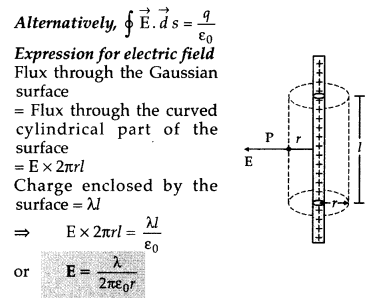1ϵ0 times the charge enclosed by the surface.

Question 62.
(a) Using Gauss’ law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density a C/m2. Draw the field lines when the charge density of the sphere is
(i) positive,
(ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 µC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere 
Answer:
(a) (i) To find out electric field at a point outside a spherical charged shell we imagine a symmetrical Gaussian surface in such a way that the point lies on it.

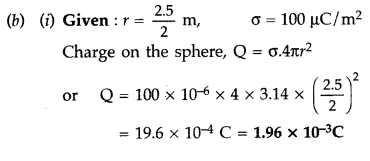
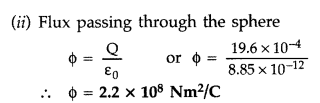
Question 63.
(a) Define electric flux. Write its SI units.
(b) The electric field components due to a charge inside the cube of side 0.1 m are as shown :
Ex = ax, where α = 500 N/C-m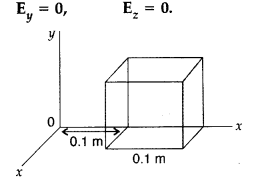

Calculate
(i) the flux through the cube, and
(ii) the charge inside the cube. 
Answer:
(a) Electric flux through a surface represents the total number of electric lines of force crossing the surface.
∴ S.I. unit is Nm2 C-1.
(b) (i) Flux through R.H.S. of the cube is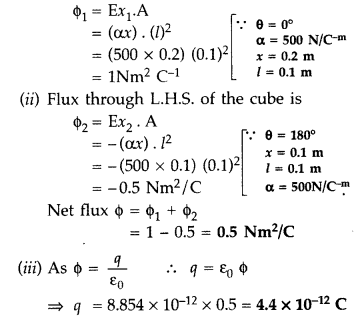

Question 64.
(a) Define electric flux. Write its S.I. units.
(b) Using Gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
(c) How is the field directed if
(i) the sheet is positively charged,
(ii) negatively charged? 
Answer:
(a) Electric flux: The electric flux through a given area held inside an electric field is the measure of the total number of electric lines of force passing normally through that area.

(b) Consider a thin, infinite plane sheet of charge with uniform surface charge density 0. We wish to calculate its electric field at a point P at distance r from it.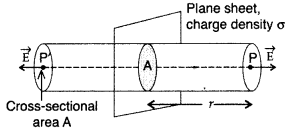

By symmetry, electric field E points outwards normal to the sheet. Also, it must have same magnitude and opposite direction at two points P anel F equidistant from the sheet and on opposite sides. We choose cylindrical Gaussian surface of cross¬sectional area A and length 2r with its axis perpendicular to the sheet.

As the lines of force are parallel to the curved surface of the cylinder, the flux through the curved surface is zero. The flux through the plane-end faces of the cylinder is :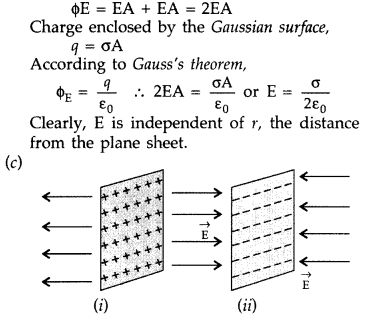

(i) For positively charged sheet ➝ away from the sheet
(ii)For negatively charged sheet ➝towards the sheet

Question 65.
(a) Define electric flux. Write its S.I. unit.
(b) A small metal sphere carrying charge +Q is located at the centre of a spherical cavity inside a large uncharged metallic spherical shell as shown in the figure the expressions for the electric field at points P1 and P2.
(c) Draw the pattern of electric field lines in this arrangement.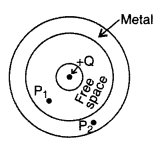 

Answer:
(a) Electric flux: The electric flux through a given area held inside an electric field is the measure of the total number of electric lines of force passing normally through that area.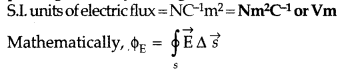

(b) Consider a thin, infinite plane sheet of charge with uniform surface charge density 0. We wish to calculate its electric field at a point P at distance r from it.

By symmetry, electric field E points outwards normal to the sheet. Also, it must have same magnitude and opposite direction at two points P anel F equidistant from the sheet and on opposite sides. We choose cylindrical Gaussian surface of cross-sectional area A and length 2r with its axis perpendicular to the sheet.

As the lines of force are parallel to the curved surface of the cylinder, the flux through the curved surface is zero. The flux through the plane-end faces of the cylinder is :

(i) For positively charged sheet ➝ away from the sheet
(ii)For negatively charged sheet ➝towards the sheet

(b) Calculation of electric field at point Pt:
Net charge enclosed by the Gaussian surface is +Q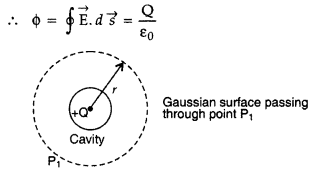

As electric field of positive charge is radially outwards, it is parallel to the area vector on the surface chosen.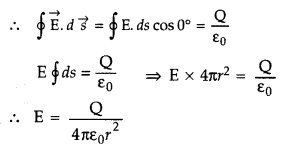

As point P2 lies inside the metal, therefore electric field at point P2 is zero.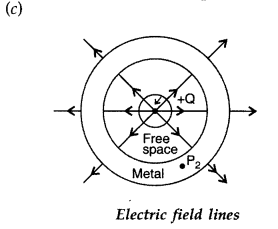

Question 66.
Define electric dipole moment. Is it a scalar or a vector? Derive the expression for the electric field of a dipole at a point on the equatorial
plane of the dipole. Answer:
Electric dipole moment: It is the product of the magnitude of either charge and distance between them.

It is a vector quantity whose direction is from negative to positive charge.

Electric field intensity at P due to +q charge is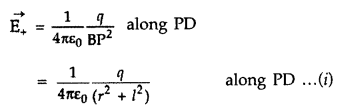

Electric field intensity at P due to -q charge is,

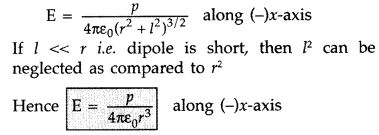
Question 67.
Using Gauss’ law deduce the expression for the electric field due to a uniformly charged spherical conducting shell of radius R at a point
(i) outside and
(ii) inside the shell.
Plot a graph showing variation of electric field as a function of r > R and r < R (r being the distance from the centre of the shell) 

Answer:

(i) Field Outside Shell :
Consider a thin spherical shell of radius R with centre O. Let charge +q be distributed uniformly over the surface of shell. To calculate electric field intensity at P where OP = r, imagine a sphere S, with centre at O and radius r. The surface of sphere is Gaussian surface over at every point. Electric field is same and directed radially outwards.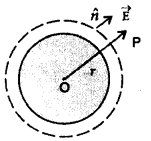

Applying Gauss’ theorem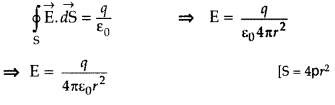

r→ is distance of point P from centre where E is calculated]
(ii) Inside Shell: As we know charge is located on its surface,

(iii) at r < R 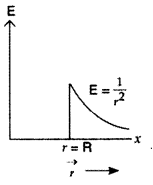E→ is zero and r  = R, E is maximum at r > R, E is decreasing at E ∝ 1r2

Question 68.
Using Gauss’s law, derive the expression for the electric field at a point
(i) outside and
(ii) inside a uniformly charged thin spherical shell. Draw a graph showing electric field E as a function of distance from the centre. 
Answer:
Electric field due to a uniformly charged spherical shell:
Suppose a thin spherical shell of radius R and centre O
Let the charge + q be distributed over the surface of sphere
Electric field intensity E→ is same at every point on the surface of sphere directed directly outwards
Let a point P be outside the shell with radius vector

Question 69.
(a) Deduce the expression for the torque acting on a dipole of dipole moment p→ in the presence of a uniform electric field E.
(b) Consider two hollow concentric spheres, S1 and S2, enclosing charges 2Q and 4Q respectively as shown in the figure.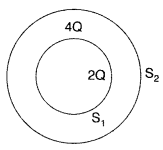

(i) Find out the ratio of the electric flux through them.
(ii) How will the electric flux through the sphere S1 change if a medium of dielectric constant ‘εr‘ is introduced in the space inside S1, in place of air? Deduce the necessary expression.
Answer:
(a) Torque on electric dipole. Consider an electric dipole consisting of two equal and opposite point charges separated by a small distance 2a, having a dipole moment

So net force on the dipole is zero
Since "E" is uniform, the dipole does not undergo any translatory motion.

These forces being equal, unlike and parallel, from a couple, which rotates the dipole in clock-wise direction
∴ Magnitude of torque = Force × arm of couple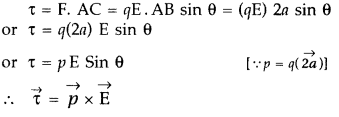

[The direction of τ⃗  is given by right hand screw rule and is normal to p⃗   ] and E⃗ 
Special cases
(i) when θ = 0 then τ = PE sin θ = 0
∴ Torque is zero and the dipole is in stable equilibrium
(ii) When θ = 90 then τ = PE sin 90 = PE
∴ The Torque is maximum
(b) Ratio of flux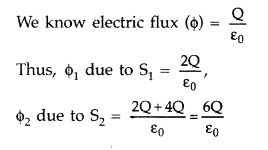


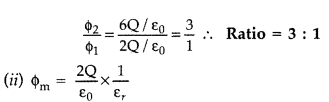
∴ Electric flux through the sphere S1 decreases with the introduction of dielectric inside it.

Question 70.
(a) An electric dipole of dipole moment p→ consists of point charges + q and – q separated by a distance 2a apart. Deduce the expression for the electric field E→ due to the dipole at a distance x from the centre of the dipole on its axial line in terms of the dipole moment p→?. Hence show that in the limit x >> a, E→ —>2p→ (4πε0x3).

Answer:
(a) Expression for magnetic field due to dipole on its axial line: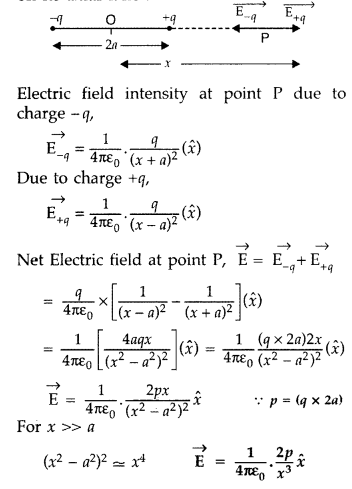

(b)Only the faces perpendicular to the direction of x-axis, contribute to the Electric flux. The remaining faces of the cube given zero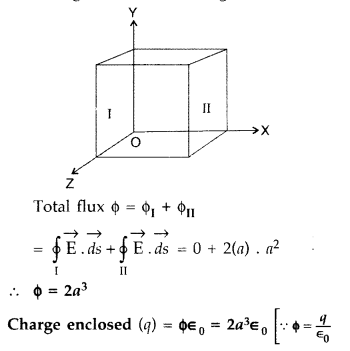

Question 71.
(a) Define electric flux. Write its S.I. unit. “Gauss’s law in electrostatics is true for any closed surface, no matter what its shape or size is”. Justify this statement with the help of a suitable example.
(b) Use Gauss’s law to prove that the electric field inside a uniformly charged spherical shell is zero. 
(a) Electric flux. The electric lines of force passing through that area, when held normally to the lines of force.
Answer:
Electric flux. The electric lines of force passing through that area, when held normally to the lines of force.

S.I. units: Vm, Nm2C-1
Gauss’s Law states that the electric flux through a closed surface is given by

The law implies that the total electric flux through a closed surface depends on the quantity of total charge enclosed by the surface, and does not depend on its shape and size.

For example, net charge enclosed by the electric dipole (q, -q) is zero, hence the total elec¬tric flux enclosed by a surface containing electric dipole is zero.
(b) Electrical field inside a uniformly charged spherical shell. Let us consider a point ‘P’ inside the shell. The Gaussian surface is a sphere through P centred at O.

The flux through the Gaussian surface is E × 4πr2.

However, in this case, the Gaussian surface encloses no charge. Gauss’s law then gives
E × 4πr2 = 0
or E = 0
(r < R)
that is, the field due to a uniformly charged thin shell is zero at all points inside the shell.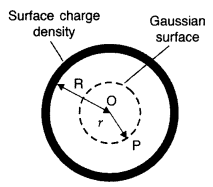

Question 72.
(a) Derive the expression for the energy stored in a parallel plate capacitor. Hence obtain the expression for the energy density of the electric field.
(b) A fully charged parallel plate capacitor is connected across an uncharged identical capacitor. Show that the energy stored in the combination is less than that stored initially in the single capacitor. 
Answer:
(a) (i) Energy of a parallel plate capacitor. Consider a capacitor of capacitance C. Initial charge on plates is zero. Initial potential difference between the capacitor plates is zero. Let a charge Q be given to it in small steps. When charge is given to capacitor, the potential difference between its plates increases. Let at any instant when charge on capacitor be q, the potential difference between its plates be,

Now work done in giving an additional infinitesimal charge dq to capacitor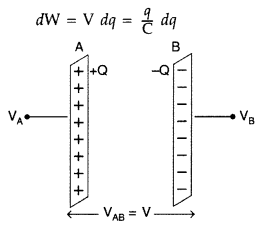

The total work done in giving charge from 0 to Q will be equal to the sum of all such infinitesimal works, which may be obtained by integration. Therefore total work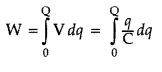


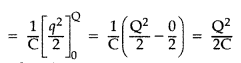
If V is the final potential difference between capacitor plates, then Q = CV

This work is stored as electrostatic potential energy of capacitor i.e., Electriostatic potential energy,

(ii) Expression for Energy Density.
Consider a parallel plate capacitor consisting of plates, each of area A, separated by a distance d. If space between the plates is filled with a medium of dielectric constant K, then
Capacitence of Capacitor,

If σ is the surface charge density of plates, then electric field strength between the plates.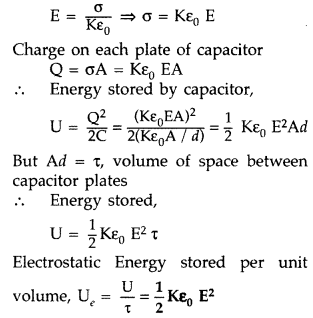

This is the expression for electrostatic energy density in medium of dielectric constan K. In air of free space  (K = 1), therefore energy density,

(b) The energy of the capacitor when fully charged is

When this charged capacitor is connected to an identical capacitor C, then the charge will be distributed equally, q2 on each of the capacitors, then


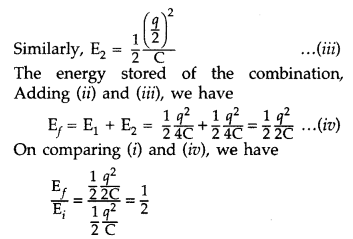
Hence, the total energy stored is half of that stored initially in one capacitor which means the energy stored in combination is less than that stored initially in the single capacitor.

Question 73.
(i) Use Gauss’s law to find the electric field due to a uniformly charged infinite plane sheet. What is the direction of field for positive and negative charge densities?
(ii) Find the ratio of the potential differences that must be applied across the parallel and series combination of two capacitors Cj and C2 with their capacitances in the ratio 1 : 2 so that the energy stored in the two cases becomes the same. 
Answer:
(i)
(a) Electric flux: The electric flux through a given area held inside an electric field is the measure of the total number of electric lines of force passing normally through that area.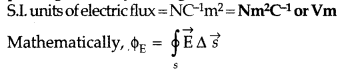

(b) Consider a thin, infinite plane sheet of charge with uniform surface charge density 0. We wish to calculate its electric field at a point P at distance r from it.

By symmetry, electric field E points outwards normal to the sheet. Also, it must have same magnitude and opposite direction at two points P anel F equidistant from the sheet and on opposite sides. We choose cylindrical Gaussian surface of cross¬sectional area A and length 2r with its axis perpendicular to the sheet.

As the lines of force are parallel to the curved surface of the cylinder, the flux through the curved surface is zero. The flux through the plane-end faces of the cylinder is :

(i) For positively charged sheet ➝ away from the sheet
(ii)For negatively charged sheet ➝towards the sheet

(b) and

Question 74.
(a) Derive an expression for the electric field E due to a dipole of length ‘2a’ at a point distant r from the centre of the dipole on the axial line. (b) Draw a graph of E versus r for r >> a.
(c) If this dipole were kept in a uniform external electric field diagrammatically represent the position of the dipole in stable and unstable equilibrium and write the expressions for the torque acting on the dipole in both the cases. 
Answer:
(a) Expression for magnetic field due to dipole on its axial lane: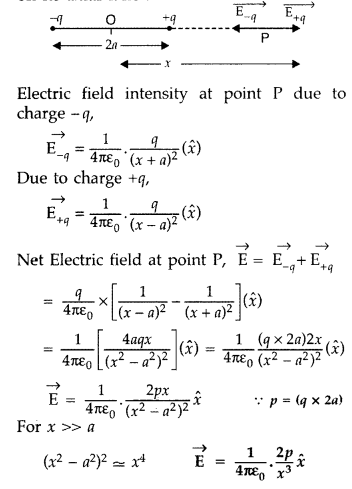

(b)Only the faces perpendicular to the direction of the x-axis contribute to the Electric flux. The remaining faces of the cube are given zero

(b) Graph between E Vs r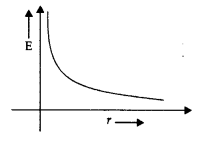

(i) Diagrammatic representation
(ii) Torque acting on these cases
(i) In stable equilibrium, torque is zero (θ = 0)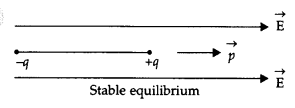

(ii) In unstable equilibrium, also, torque is zero (θ = 180°)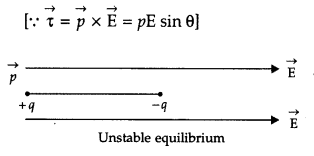

Question 75.
(a) Use Gauss’s theorem to find the electric field due to a uniformly charged infinitely large plane thin sheet with surface charge density a.
(b) An infinitely large thin plane sheet has a uniform surface charge density +a. Obtain the expression for the amount of work done in bringing a point charge q from infinity to a point, distant r, in front of the charged plane sheet. 

Answer:
(a) Electric flux: The electric flux through a given area held inside an electric field is the measure of the total number of electric lines of force passing normally through that area.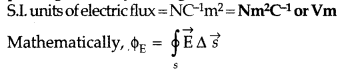

(b) Consider a thin, infinite plane sheet of charge with uniform surface charge density 0. We wish to calculate its electric field at a point P at a distance r from it.

By symmetry, the electric field E points outwards normal to the sheet. Also, it must have the same magnitude and opposite direction at two points P and F equidistant from the sheet and on opposite sides. We choose cylindrical Gaussian surface of cross¬sectional area A and length 2r with its axis perpendicular to the sheet.

As the lines of force are parallel to the curved surface of the cylinder, the flux through the curved surface is zero. The flux through the plane-end faces of the cylinder is :

(i) For positively charged sheet ➝ away from the sheet
(ii)For negatively charged sheet ➝towards the sheet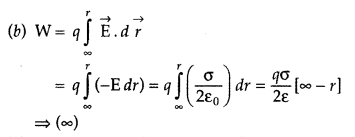

Question 76.
(a) State Gauss’ law. Using this law, obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density X.
(b) A wire AB of length L has linear charge density λ = kx, where x is measured from the end A of the wire. This wire is enclosed by a Gaussian hollow surface. Find the expression for the electric flux through this surface.

Answer:
(a)
Gauss’s law in electrostatics: It states that “the total electric flux over the surface S in vacuum is 1ε0 times the total charge (q).”

Electric field due to an infinitely long straight wire: Consider an infinitely long straight line charge having linear charge density X to determine its electric field at a distance r. Consider a cylindrical Gaussian surface of radius r and length l coaxial with the charge. By symmetry, the electric field E has the same magnitude at each point of the curved surface Sj and is directed radially outward.
Total flux through the cylindrical surface,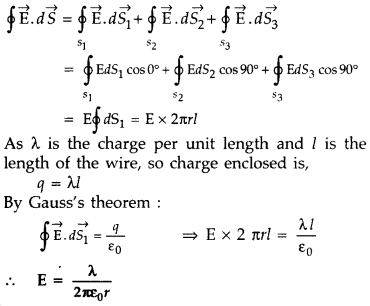

(b) Given : Length of wire = L, Charge density (λ) = kx, ϕ = ?
We know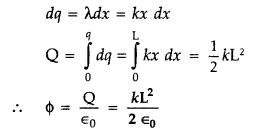

Question 77.
Two point charges 4 (J.C and +1 pC are separated by a distance of 2 m in air. Find the point on the line joining charges at which the net electric field of the system is zero. 
Answer:
q1 = 4 µC, q2 = 1 µC, r = 2 m
At this point, the net electric field of the system is zero.